Original Source Here

Bitcoin Price Prediction with RNN and LSTM in Python

Prediction of Bitcoin Prices Using Deep Learning

Prediction of bitcoin. A photo by Author

In this article, we will discuss a program related to Bitcoin Price Prediction.

We will be discussing the libraries used here too with graphical representations.

Topics to be covered:

1. What is a Bitcoin
2. How to use Bitcoin
3. Prediction of Bitcoin Prices Using Deep Learning

What is a Bitcoin?

Bitcoin is one of the cryptocurrencies used commonly by all crypto enthusiasts. Even though there are several cryptocurrencies like Ethereum, Ripple, Litecoin, etc, Bitcoin ranks on the top lists.

Cryptocurrencies are commonly used as an encrypted form of our currency are widely used for shopping, trading, investments, etc.

It uses peer-to-peer technology. The reason behind this technology is that there is no driving force or any 3rd parties to interfere with the transactions done within the network. Moreover, Bitcoin is “open-source” and it can be used by anyone.

Some of the features are:

1. Fast peer-to-peer transactions
2. Worldwide payments
3. Low processing fees

Principle Used — Cryptography:

The working principle behind the cryptocurrency (Bitcoin) is “cryptography”. They work using this principle to secure and authenticate negotiation as well as to control the establishment of a new component of cryptocurrency.

Flow chart steps on bitcoin. Source is techtarget

How to Use Bitcoin?

Secure the wallet: Bitcoin wallet should be kept more secured for easy and smooth transactions
Bitcoin Price is volatile: There can be fluctuations in the prices of Bitcoin. The price can either increase or decrease depending upon several factors like inflation rate, volume, etc.

Prediction of Bitcoin Prices Using Deep Learning:

The steps used in this project are:

1. Data Collection:

Importing the CSV file dataset.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

Now, importing the data set with pandas and numpy. Numpy is used mainly for scientific computing in python

coindata = pd.read_csv(‘Dataset.csv’)
googledata = pd.read_csv(‘DS2.csv’)

Now the loaded raw data sets are printed

coindata = coindata.drop([‘#’], axis=1)
coindata.columns = [‘Date’,’Open’,’High’,’Low’,’Close’,’Volume’]
googledata = googledata.drop([‘Date’,’#’], axis=1)

Unused columns are dropped here. Here, we drop two columns from coin data and google data sets as they are unused columns.

Now, the final results are printed for the two datasets after removing the unused columns from the datasets.

last = pd.concat([coindata,googledata], axis=1)

Now, the two datasets — coin data and google data are concatenated and it is printed using the function

last.to_csv(‘Bitcoin3D.csv’, index=False)

The final dataset is now exported after the concatenation of the two data sets.

1. RNN for 1D:

import pandas as pd
import matplotlib.pyplot as plt
import numpy as npimport mathfrom sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_errorfrom keras.models import Sequential
from keras.layers import Dense, Activation, Dropout
from keras.layers import LSTM

Here, we use Keras libraries. Keras is used to train the neural network model with efficient computational libraries in just a few lines of code.MinMaxScaler will transform the features by mapping each feature to a given range. The sklearn package will provide some utility functions required for the program.

Dense layer will be doing the below operation and will return the output.

output = activation(dot(input, kernel) + bias)def new_dataset(dataset, step_size):
    data_X, data_Y = [], []
    for i in range(len(dataset)-step_size-1):
        a = dataset[i:(i+step_size), 0]
        data_X.append(a)
        data_Y.append(dataset[i + step_size, 0])
    return np.array(data_X), np.array(data_Y)

Here, we are framing up the 1D data that we had collected during the Data Preprocessing stage into Time Series Data

df = pd.read_csv(“Bitcoin1D.csv”)
df[‘Date’] = pd.to_datetime(df[‘Date’])
df = df.reindex(index= df.index[::-1])

The data sets are loaded. The feature is read from the Bitcoin1D.csv file. Also, we convert the Date column to DateTime. Reindex all the datasets by the Date column.

zaman = np.arange(1, len(df) + 1, 1)
OHCL_avg = df.mean(axis=1)

Here, we directly assign a new index array.

OHCL_avg = np.reshape(OHCL_avg.values, (len(OHCL_avg),1)) #7288 data
scaler = MinMaxScaler(feature_range=(0,1))
OHCL_avg = scaler.fit_transform(OHCL_avg)

Normalize the data sets after assigning the scaler

#print(OHCL_avg)train_OHLC = int(len(OHCL_avg)*0.56)
test_OHLC = len(OHCL_avg) — train_OHLCtrain_OHLC, test_OHLC = OHCL_avg[0:train_OHLC,:], OHCL_avg[train_OHLC:len(OHCL_avg),:]#Train the datasets and test ittrainX, trainY = new_dataset(train_OHLC,1)
testX, testY = new_dataset(test_OHLC,1)

We create the 1D dimension dataset from mean OHLC (Open High Low Close)

trainX = np.reshape(trainX, (trainX.shape[0],1,trainX.shape[1]))
testX = np.reshape(testX, (testX.shape[0],1,testX.shape[1]))step_size = 1

Now, reshape the dataset for LSTM in 3D dimension. Assign the step_size to 1.

model = Sequential()
model.add(LSTM(128, input_shape=(1, step_size)))
model.add(Dropout(0.1))
model.add(Dense(1))
model.add(Activation(‘linear’))

Here, LSTM Model is created

model.compile(loss=’mean_squared_error’, optimizer=’adam’)
model.fit(trainX, trainY, epochs=10, batch_size=25, verbose=2)

We define the number of epochs to 10, batch_size to 25

trainPredict = model.predict(trainX)
testPredict = model.predict(testX)trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)testY = scaler.inverse_transform([testY])

Now, De-Normalization is done for plotting

trainScore = math.sqrt(mean_squared_error(trainY[0], 
                       trainPredict[:,0]))testScore = math.sqrt(mean_squared_error(testY[0], 
                       testPredict[:,0]))

Performance Measure RMSE is calculated for the predicted test dataset

trainPredictPlot = np.empty_like(OHCL_avg)trainPredictPlot[:,:] = np.nantrainPredictPlot[step_size:len(trainPredict)+step_size,:] =
                                                  trainPredict

Now, the converted train data set are used for plotting

testPredictPlot = np.empty_like(OHCL_avg)testPredictPlot[:,:] = np.nantestPredictPlot[len(trainPredict)+(step_size*2)+1:len(OHCL_avg)-1,:]
                    = testPredict

Now, the converted predicted test dataset is used for plotting

Finally predicted values are visualized

OHCL_avg = scaler.inverse_transform(OHCL_avg)plt.plot(OHCL_avg, ‘g’, label=’Orginal Dataset’)
plt.plot(trainPredictPlot, ‘r’, label=’Training Set’)
plt.plot(testPredictPlot, ‘b’, label=’Predicted price/test set’)
plt.title(“ Bitcoin Predicted Prices”)
plt.xlabel(‘ Time’, fontsize=12)
plt.ylabel(‘Close Price’, fontsize=12)
plt.legend(loc=’upper right’)
plt.show()

Output of 1D — RNN. A photo by Author

3. RNN for multi-variant:

import pandas as pd
from pandas import DataFrame
from pandas import concatfrom math import sqrt
from numpy import concatenateimport matplotlib.pyplot as pyplot
import numpy as npfrom sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScalerfrom keras import Sequential
from keras.layers import LSTM, Dense, Dropout, Activationfrom pandas import read_csv

Here, we use Keras libraries. Keras is used to train the neural network model with efficient computational libraries in just a few lines of code. The sklearn package will provide some utility functions required for the program.

The dense layer will be doing the below operation and will return the output.

dataset = read_csv(‘Bitcoin3D.csv’, header=0, index_col=0)
print(dataset.head())values = dataset.values

Loads the dataset by using Pandas Library. Here was prepared the column for visualizing.

groups = [0, 1, 2, 3, 5, 6,7,8,9]
i = 1

Convert the series to supervised learning

def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
    n_vars = 1 if type(data) is list else data.shape[1]
    df = DataFrame(data)
    cols, names = list(), list()
    # Here is created input columns which are (t-n, … t-1)
    for i in range(n_in, 0, -1):
        cols.append(df.shift(i))
        names += [(‘var%d(t-%d)’ % (j+1, i)) for j in range(n_vars)]#Here, we had created output/forecast column which are (t, t+1, … t+n)
    for i in range(0, n_out):
        cols.append(df.shift(-i))
        if i == 0:
            names += [(‘var%d(t)’ % (j+1)) for j in range(n_vars)]
        else:
            names += [(‘var%d(t+%d)’ % (j+1, i)) for j in
                                             range(n_vars)]    agg = concat(cols, axis=1)
    agg.columns = names
    # drop rows with NaN values 
    if dropnan:
        agg.dropna(inplace=True)
    return agg

Check if the values are in numeric format

values = values.astype(‘float32’)

The Dataset values are normalized by using MinMax method

scaler = MinMaxScaler(feature_range=(0,1))
scaled = scaler.fit_transform(values)

The Normalized values are converted for supervised learning

reframed = series_to_supervised(scaled,1,1)#reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True)

Dataset is split into two groups which are train and test sets

values = reframed.values
train_size = int(len(values)*0.70)
train = values[:train_size,:]
test = values[train_size:,:]

Split datasets are split to trainX, trainY, testX and testY

trainX, trainY = train[:,:-1], train[:,13]
testX, testY = test[:,:-1], test[:,13]

Train and Test datasets are reshaped in 3D size to be used in LSTM

trainX = trainX.reshape((trainX.shape[0],1,trainX.shape[1]))
testX = testX.reshape((testX.shape[0],1,testX.shape[1]))

LSTM model is created and adjusted neuron structure

model = Sequential()
model.add(LSTM(128, input_shape=(trainX.shape[1], trainX.shape[2])))
model.add(Dropout(0.05))
model.add(Dense(1))
model.add(Activation(‘linear’))
model.compile(loss=’mae’, optimizer=’adam’)

Dataset is trained by using trainX and trainY

history = model.fit(trainX, trainY, epochs=10, batch_size=25, validation_data=(testX, testY), verbose=2, shuffle=False)

Loss values are calculated for every training epoch and are visualized

pyplot.plot(history.history[‘loss’], label=’train’)
pyplot.plot(history.history[‘val_loss’], label=’test’)
pyplot.title(“Test and Train set Loss Value Rate”)
pyplot.xlabel(‘Epochs Number’, fontsize=12)
pyplot.ylabel(‘Loss Value’, fontsize=12)
pyplot.legend()
pyplot.show()

Loss graph. A photo by Author

The Prediction process is performed for the training dataset

trainPredict = model.predict(trainX)
trainX = trainX.reshape((trainX.shape[0], trainX.shape[2]))

The prediction process is performed for the test dataset

testPredict = model.predict(testX)
testX = testX.reshape((testX.shape[0], testX.shape[2]))

Trains dataset inverts scaling for training

trainPredict = concatenate((trainPredict, trainX[:, -9:]), axis=1)
trainPredict = scaler.inverse_transform(trainPredict)
trainPredict = trainPredict[:,0]

Test dataset inverts scaling for forecasting

testPredict = concatenate((testPredict, testX[:, -9:]), axis=1)
testPredict = scaler.inverse_transform(testPredict)
testPredict = testPredict[:,0]# invert scaling for actualtestY = testY.reshape((len(testY), 1))
inv_y = concatenate((testY, testX[:, -9:]), axis=1)
inv_y = scaler.inverse_transform(inv_y)
inv_y = inv_y[:,0]

Performance measures are calculated by using mean_squared_error for train and test prediction

rmse2 = sqrt(mean_squared_error(trainY, trainPredict))rmse = sqrt(mean_squared_error(inv_y, testPredict))

The trained and test predicted sets are concatenated

final = np.append(trainPredict, testPredict)final = pd.DataFrame(data=final, columns=[‘Close’])
actual = dataset.Close
actual = actual.values
actual = pd.DataFrame(data=actual, columns=[‘Close’])

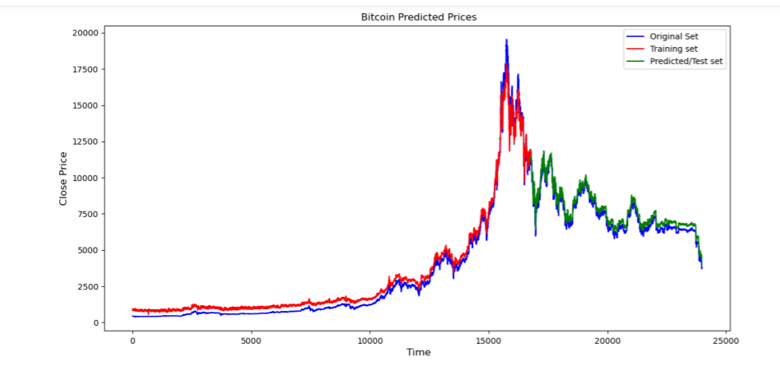
Finally, training and prediction results are visualized

pyplot.plot(actual.Close, ‘b’, label=’Original Set’)
pyplot.plot(final.Close[0:16781], ‘r’ , label=’Training set’)pyplot.plot(final.Close[16781:len(final)], ‘g’,
            label=’Predicted/Test set’)pyplot.title(“ Bitcoin Predicted Prices”)
pyplot.xlabel(‘ Time’, fontsize=12)
pyplot.ylabel(‘Close Price’, fontsize=12)
pyplot.legend(loc=’best’)
pyplot.show()

Output of RNN multi-variant. A photo by Author

Conclusion:

Here we develop a price prediction model using the historical bitcoin price data set. We use the RNN and LSTM algorithms to find the price prediction.

I hope you like the article. Reach me on my LinkedIn and twitter.