Hierarchical clustering explained

Original Source Here

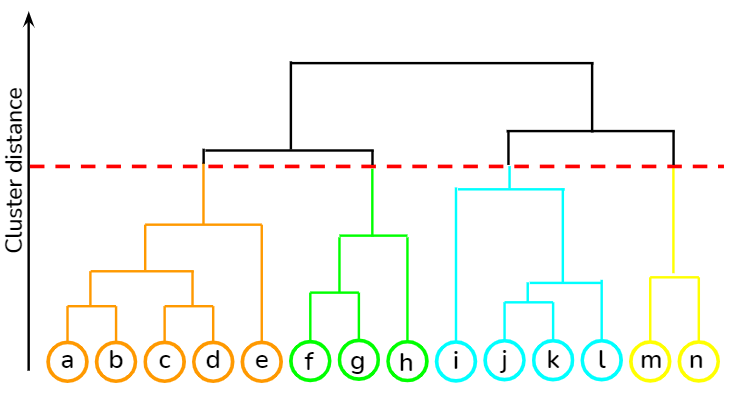
Interpretation of dendrogram

Each level of dendrogram has a subtle meaning to the relationship between its data members. In a regular relationship chart, one may interpret that at the top lies grandparents or the first generation, the next level corresponds to parents or second generation and the final level belongs to children or third generation. Likewise, in every branching procedure of dendrogram, all the data points having the membership at each level belongs to a certain class.

However, to infer this class entity, one has to go through a few individual samples of each level within the formulated cluster and find out what feature is common in the resulting cluster. Also, these inferred classes need not be similar at the sister branches. For example, in level 2, the cats have been clustered on big ears and calm behavior but dogs have been clustered on a similar attribute of size.

Inferred classes of data in dendrogram by the user (Image by Author)

Construction of dendrogram

Now that we have understood what a dendrogram is, let us learn how to construct it. There are two ways of constructing it. One way to construct it is by bottoms-up where you start from the bottom and keep merging the individual data points and subclusters and go all the way to the top. This is known as agglomerative clustering.

The other alternative is the opposite procedure of top-down in which you start by considering the entire system as one cluster and then keep sub clustering it until you reach individual data samples. This process is known as divisive clustering. Each of these methods has separate algorithms to achieve its objectives.

a) Agglomerative clustering

One of the simplest and easily understood algorithms used to perform agglomerative clustering is single linkage. In this algorithm, we start with considering each data point as a subcluster. We define a metric to measure the distance between all pairs of subclusters at each step and keep merging the nearest two subclusters in each step. We repeat this procedure till there is only one cluster in the system.

b) Divisive clustering

One of the algorithms used to perform divisive clustering is recursive k-means. As the name suggests, you recursively perform the procedure of k-means on each intermediate cluster till you encounter all the data samples in the system or the minimum number of data samples you desire to have in a cluster. In each step of this algorithm, you have to be mindful of how many clusters would you like to create next.

Formation of agglomerative/divisive cluster with data samples represented by black dots (Image by Author)

In both the clustering approaches, when we are drawing the dendrogram, we have to be mindful of the distance between the two subsuming clusters, and the variation in the scale of the distance is maintained in the Y-axis of the dendrogram diagram.

Variation in height of branch in dendrogram based on cluster distance (Image by Author)

Lastly, let us look into the advantages and disadvantages of hierarchical clustering.

Advantages

• With hierarchical clustering, you can create more complex shaped clusters that weren’t possible with GMM and you need not make any assumptions of how the resulting shape of your cluster should look like.

Complex structured shapes formed with hierarchical clustering (Image by Author)

• In one go, you can cluster the dataset first at various levels of granularity, and then decide upon the number of clusters you desire in your dataset.
• If you are using some type of Minkowski distance, say Euclidean distance to measure the distance between your clusters, then mathematically, your clustering procedure can become very easy to understand.

Disadvantages

• When you begin analyzing and taking decisions on dendrograms, you will realize that hierarchical clustering is heavily driven by heuristics. This leads to a lot of manual intervention in the process and consequently, application/domain-specific knowledge is required to analyze whether the result makes sense or not.
• Though hierarchical clustering may be mathematically simple to understand, it is a mathematically very heavy algorithm. In any hierarchical clustering algorithm, you have to keep calculating the distances between data samples/subclusters and it increases the number of computations required.
• The last disadvantage that we will list is one of the biggest detrimental factors on why hierarchical clustering is usually shunned away by ML engineers. In all our visualizations, we have shown dendrograms having very few data samples. If the number of data samples increases (and quite possibly every time), then visually analyzing dendrogram and making decisions becomes impossible.

In this article, we have explored the concepts of hierarchical clustering. Do share your views in the comments section.

AI/ML

Trending AI/ML Article Identified & Digested via Granola by Ramsey Elbasheer; a Machine-Driven RSS Bot

via WordPress https://ramseyelbasheer.io/2021/05/08/hierarchical-clustering-explained/