How the Dot Product Measures Similarity

The geometric explanation behind cosine similarity

The dot product is one of the most fundamental concepts in machine learning, making appearances almost everywhere.

One of its most important applications is to measure similarity between feature vectors.

But how is similarity and inner product are related? The definition doesn’t reveal much. In this post, our goal is to unravel the dot product and provide a simple geometric explanation!

The fundamental properties of dot product

To see what the dot product has to do with similarity, we have three key observations.

First, we can see that it is linear in both variables. (This property is called bilinearity.)

Second, the dot product of orthogonal vectors is zero.

Third, the dot product of a vector with itself equals the square of its magnitude.

Armed with these properties, we are ready to explore how similarity is measured!

Dot product as similarity

Suppose that we have two vectors, x and y. To see the geometric interpretation of their dot product, we first note that x can be decomposed into the sum of two components: one is parallel to y, while the other is orthogonal.

So, the dot product of x and y equals to the one with xᵧ and y. If we write xᵧ as a scalar multiple of y, we can simplify a lot.

We can go even one step further. If we assume that both x and y have a magnitude of one, the dot product equals to the scaling factor!

Note that this scaling factor is in the interval [-1, 1]. It can be negative if the directions of xᵧ and y are the opposite.

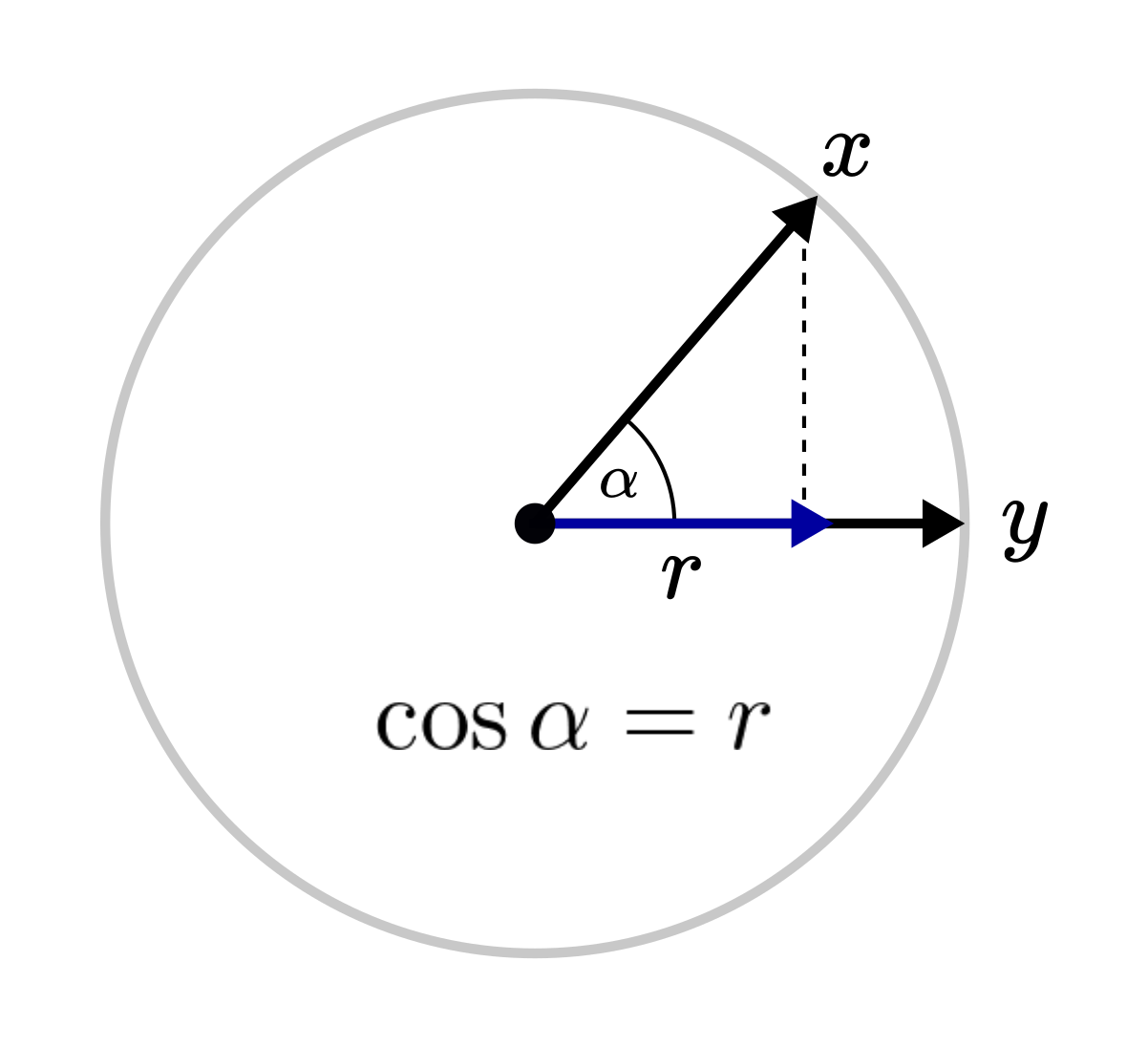
Now comes the really interesting part! r has a simple geometric meaning. To see this, let’s illustrate what is happening. (Recall we assumed that x and y both have a magnitude of one.)

Since cosine is defined by the ratio of the adjacent side and the hypotenuse, it turns out that the scaling factor r also equals to the cosine of the angle between x and y.

It is the reason why cosine similarity is defined this way.

I hope that this short post helps you make sense of this concept, and armed with this knowledge, you’ll be more confident when dealing with it!

AI/ML

Trending AI/ML Article Identified & Digested via Granola by Ramsey Elbasheer; a Machine-Driven RSS Bot

via WordPress https://ramseyelbasheer.io/2021/04/21/how-the-dot-product-measures-similarity/