Overparameterized but generalized ~ Neural Network
Original Source Here
Overparameterized but generalized ~ Neural Network
Why does your deep neural network perform well on test data?
Deep learning has evolved from just being parameterized non linear functions to being used in major computer vision and natural language processing tasks. The piecewise non linear networks are able to form non trivial representations of data. Though, these networks have been highly successful there are many gaps between their understanding of why they perform so well by finding near optimal solutions to problems.
These models give 0 training error, therefore highly overfitting the training data but are still able to give good test performance.
This benign overfitting appears to contradict accepted statistical wisdom, which insists on a trade-off between the complexity of a model and its fit to the data. Therefore it becomes necessary to examine this interesting phenomenon to fill in the gaps.
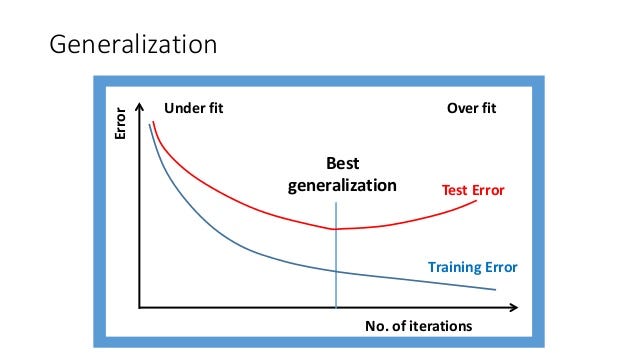
What is generalization?
Suppose our task is to map a set of data points X to their labels Y. We define a function f: X->Y. The underlying assumption here is that the data is i.i.d which means each data point was generated independent randomly of each other.
There can be many ways to choose f. One of the ways could be to let the data distribution X decide what f should be, let’s say this is f^. Now we would want f^ to give good predictions such that the risk of f^
is minimum. Risk is basically the expectation of the loss. Is there a way to guarantee that
the output is small for large sample size n. Here f* is the best function which describes the data.
This gives us a measure of how good our model will perform on unknown samples. One thing to note here is that if we have enough number of samples, both these terms will converge.
But in real life this is not the case. We need to know how many mistakes our model will make with n number of samples on a a particular model, thus how good our model will ‘Generalize’.
Generalization gives us a bound of the highest number of mistakes our model will perform without seeing the data.
Don’t you think this is super important for models in production? We can find out the highest numbers of mistakes our model would make!
Generalization Methods
Traditional approaches to generalization take a Model Capacity point of view where the ability to generalize is modeled by the complexity (capacity) of a hypothesis class H. Where Hypothesis class is all the possible functions f (see first section) that could fit the data. Some of the traditions approaches include VC dimension, Rademacher complexity and PAC-Bayes bounds.
- VC dimension- Measure of the capacity of a set of functions that can be learned by an algorithm. It is measured by the largest set of points that the algorithm can shatter. f is said to shatter a set of data points if for all assignments of labels to those points, there exists a function such that f makes no errors on evaluating on those points.
- Rademacher complexity- Measure of richness of a class of real-valued functions, thus is the ability of a a hypothesis class to fit binary labels.
- Probably Approximately Correct- As stated in [3]
Let’s make it simple : The primary goal of PCA is to analyze whether and under what conditions a model will probably output an approximately correct classifier. Here we can define ‘approximate’ by
Where D is the distribution over inputs and h is the hypothesis. Next, how do we define “probably”? If our model will output such a classifier with probability 1−δ, with 0≤δ≤1/2, we call that classifier probably approximately correct. Knowing that the target concept is PAC-learnable, allows you to bound the sample size necessary to probably learn an approximately correct classifier.
Generalization in Neural Networks
Empirical Study of methods
There have been various theoretical and empirical results proposed by the community. [2] Did a study of 40 measures by systematically varying hyperparameters. They trained around 10000 convolution networks to understand the relationship between generalization and different hyperparameter settings. They found the potential of PAC-Bayesian bounds and the failure of norm-based measures.
Exploring Generalization through Randomized tests
The paper by Zhang et.al. [1]performed randomized test where the true labels were replaces by random labels. Ideally the model should not perform well. But to their surprise, they found ~ Deep neural networks easily fit random labels with 0 training error.
By randomizing labels alone we can force the generalization error of a model to jump up considerably without changing the model, its size, hyperparameters, or the optimizer.
They also replace the true images by completely random pixels (e.g., Gaussian noise) and observe that convolutional neural networks continue to fit the data with zero training error. This shows that despite their structure, convolutional neural nets can fit random noise.
They furthermore vary the amount of randomization, interpolating smoothly between the case of no noise and complete noise to observe a steady deterioration of the generalization error as we increase the noise level. This shows that neural networks are able to capture the remaining signal in the data, while at the same time fit the noisy part using brute-force.
Representation Learning perspective
Zhou Z-H[4] gives a very different perspective on this problem. His answer to why over-parameterization does not overfit leads to the fact that –
Deep networks combines feature learning with classifier training. All the conventional learning theory concerns mostly about the training of a learner or more specifically a classifier from a feature space, but concerns little about the construction of the feature space itself.
Therefore, conventional learning theory can be exploited to understand the behavior of generalization, but one must be careful when it is applied to representation learning. Therefore special work on generalization of learning of representations need to be done.
Empirical methods
The winning solution of NeurIPS competition on Predicting Generalization in Deep Learning (NeurIPS 2020) [5].claim that the theoretical bounds have usually proven to be not useful in the practical setting. They gives generalization errors on training data without looking at the test data. They exploit two features of representation- consistency and robustness to measure generalization. They had the following view for their approach-
If a deep neural network assigns the same label to two images, they have to converge into a similar representation at some stage of the network.
Measuring the consistency of representation inside the network would then tell us about the generalization capacity of that network.
Robustness of a model to plausible perturbations in the input space is another marker for generalization capacity.
For measuring robustness of the network representations to valid or plausible perturbations, they used Mixup. In Mixup, they check performance of the model on linear combinations of input samples within the same label.
How far away samples are from being classified into another class.
They demonstrate augmented margin distribution as a metric for generalization which can take into account overfitted and outlier samples.
Optimization perspective to generalization
Google[7] gives an online optimization perspective to generalization. They give a deep bootstrap framework where they compare the training world with limited data to an ideal world with unlimited data. A priori, one might expect the real and ideal worlds may have nothing to do with each other, since in the real world the model sees a finite number of examples from the distribution while in the ideal world the model sees the whole distribution. But in practice, they found that the real and ideal models actually have similar test error.
Training in a scenario when unlimited training data was present (ideal world) to where limited data is present (real world) gives similar test error until real world converges.
Thus, one can study models in the real world by studying their corresponding behavior in the ideal world. Good models and training procedures are those that (1) optimize quickly in the ideal world and (2) do not optimize too quickly in the real world. Whenever one makes a change that affects generalization in the real world (the architecture, learning-rate, etc.), one should consider its effect on (1) the ideal world optimization of test error (faster is better) and (2) the real world optimization of train error (slower is better).
Conclusion
Overparameterization in neural networks makes them interesting from a statistical point of view. This post gives a small introduction of traditional methods to measure generalization which do not directly work in deep learning. There have been different perspective provided from the point of view of representation learning and optimization to explain the high test performance achieved by neural nets.
[1] Understanding deep learning requires rethinking generalization (arxiv.org)
AI/ML
Trending AI/ML Article Identified & Digested via Granola by Ramsey Elbasheer; a Machine-Driven RSS Bot
via WordPress https://ramseyelbasheer.io/2021/03/28/overparameterized-but-generalized-neural-network/