Genetic Algorithm Optimization Algorithm
Original Source Here
Genetic Algorithm Optimization Algorithm
An optimization algorithm inspired by natural evolution such as selection, mutation, and cross-over
Learn about the Genetic Algorithm, what role it plays in artificial intelligence, how it works, and finally, look at an implementation.
The Genetic Algorithm(GA) is an evolutionary algorithm(EA) inspired by Charles Darwin’s theory of natural selection which espouses Survival of the fittest.
As per the natural selection theory, the fittest individuals are selected to produce offsprings. The fittest parents’ characteristics are then passed on to their offsprings using cross-over and mutation to ensure better chances of survival.
Genetic algorithms are randomized search algorithms that generate high-quality optimization solutions by imitating the biologically inspired natural selection process such as selection, cross-over, and mutation.
The objective of Genetic algorithm is to find the best-optimized solution from a search space
Terminology for Genetic Algorithm
Before we dive into the Genetic Algorithm’s workings, we will briefly understand the terms used in the Genetic Algorithm.
Generation or Population contains a set of possible solutions for the stochastic search process to begin. GA will iterate over multiple generations till it finds an acceptable and optimized solution. First-generation is randomly generated.
Chromosome represents one candidate solution present in the generation or population. A chromosome is also referred to as a Genotype.
A chromosome is composed of Genes that contain the value for the optimal variables.
Phenotype is the decoded parameter list for the genotype that is processed by the Genetic Algorithm. Mapping is applied to the genotype to convert to a phenotype.
The Fitness function or the objective function evaluates the individual solution or phenotypes for every generation to identify the fittest members.
Different Genetic Operators
Selection is the process of selecting the fittest solution from a population, and then the fittest solutions act as parents of the next generation of solutions. This allows the next generation to inherit the strong features naturally. Selection can be performed using Roulette Wheel Selection or Rank Selection based on the fitness value.
Cross-over or recombination happens when genes from the two fittest parents are randomly exchanged to form a new genotype or solution. Cross over can be a One-point cross over or Multi-Point Cross over based on the parent’s segments of genes exchanged.
After a new population is created through selection and crossover, it is randomly modified through mutation. A mutation is a process to modify a genotype using a random process to promote diversity in the population to find better and optimized solutions.
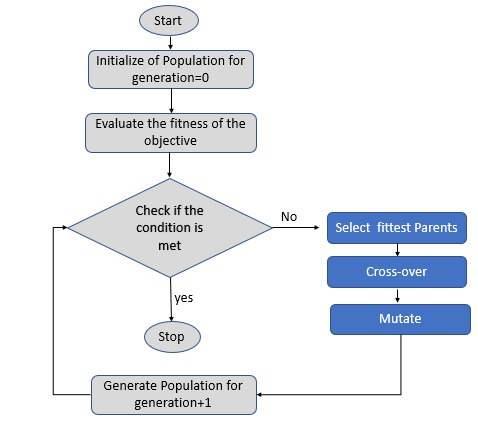
Working of Genetic Algorithm
Initialize the Population for Generation 0: GA begins with creating an initial population of randomly generated possible candidate solutions for a problem.
Evaluate each of the solutions in the generation based on the objective function or the fitness function.
Check if the termination condition is met. The termination conditions can be any of the following conditions
- when the algorithm has generated the predefined generations
- When our fitness function has reached a predefined target value
If the termination condition is not met, then Generate Population for Next-generation:
The fittest population members are identified, ranked, and selected as parents for the next generation. The genotype of the next generation is created through genetic operations like crossover and mutation.
Genetic Algorithm propagates successful solutions and should produce increasingly capable solution populations.
Usage of Genetic Algorithm in Artificial Intelligence
A Genetic Algorithm is used for Search and Optimization using an iterative process to arrive at the best solution out of multiple solutions.
- In Deep Learning, a Genetic Algorithm can efficiently find a good set of the hyperparameter and their values for a deep learning model to improve its performance.
- A Genetic Algorithm can also be used to select the optimum number of features for building a machine learning model that is important for predicting the target variable.
Strengths of the Genetic Algorithm
- A generic framework for solving the complex optimization problem.
- Explores the search space in a relatively short computation time.
- Multiple complex optimization objectives can easily be included
- Robust to local minima and maxima and easy to discover global optimum
- GA can be easily parallelized
Implementation of Genetic Algorithm
Here we will find an optimum solution to generate an array with a number ranging between 0 and 9 that will have a sum less than or equal to 11.
Importing required libraries and setting constants
import numpy as np
from random import randint, random, choice
TARGET=11
generations=1000
NO_OF_BEST_SOLUTIONS=5
NO_OF_SOLUTION_IN_A_GENERATION=10
SIZE_OF_A_SOLUTION=10
LOWER_RANGE=0
UPPER_RANGE=10
Randomly Generate a Population
def generate_population(no_of_solution, size, lower, upper):
solution = []
population=[]
for i in range(no_of_solution):
#Create a chromosome or solution for the population.
solution=[randint(lower,upper) for x in range(size) ]
population.append(solution)
return population
Define the fitness function
The fitness function will return the absolute difference between the individual solution and the predefined TARGET.
def fitness(individual):
"""
Determine the fitness of an individual. Lower is better.
individual: the individual to evaluate
"""
total_list_sum = sum(individual)
return np.abs(total_list_sum - TARGET)
Sort the population so that the individual solutions with the lowest absolute difference are on the top of the list as they are the best solutions out of the population
def sort_population_by_fitness(population):
return sorted(population, key=fitness, reverse=False)
Create a child using a cross over between two fittest parents
Cross over is created by combining genes from the two fittest parents by randomly picking a part of the first parent and a part of the second parent
#the most common technique is to pick a part of the bit string of A and a part of bit string of B
def crossover(individual_a, individual_b):
new_list=[]
first=randint(2,8)
new_list= individual_a[:first] + individual_b[first:]
return new_list
Create a child by mutation
The mutation is achieved by randomly flipping selected bits of one of the fittest parents from the population.
#you can simply flip randomly selected bits of the individual string
def mutate(individual):
new_list=[]
first=randint(0,9)
second=randint(0,9)
third=randint(0,9)
individual[first]=randint(0,9)
individual[second]=randint(0,9)
individual[third]=randint(0,9)
return individual
Create a new generation of population
A new generation is created by selecting the fittest parents from the previous generation, applying cross-over and mutation.
def make_next_generation(previous_population):
next_generation = []
sorted_by_fitness_population = sort_population_by_fitness(previous_population)
population_size = len(previous_population)
for i in range(population_size):
# find the least loss in the fitness function among the population
for j in range(0,NO_OF_BEST_SOLUTIONS):
pick_best_parents= randint(0,NO_OF_BEST_SOLUTIONS-2)
parent_1=sorted_by_fitness_population[pick_best_parents]
parent_2=sorted_by_fitness_population[pick_best_parents+1]
best_parent_1=sorted_by_fitness_population[0]
best_parent_2=sorted_by_fitness_population[1]
draw = choice(["crossover", "mutate_parent1", "mutate_parent2", "Parent 1", "Parent 2","best 1", "best 2" ])
if draw=="crossover":
individual = crossover(parent_1, parent_2)
elif draw=="mutate_parent1":
individual = mutate(parent_1)
elif draw=="mutate_parent2":
individual = mutate(parent_2)
elif draw=="Parent 1":
individual =parent_1
elif draw=="Parent 2":
individual =parent_2
elif draw=="best 1":
individual =best_parent_1
elif draw=="best 2":
individual =best_parent_2
next_generation.append(individual)
return next_generation
The Genetic Algorithm
First, we initialize the solutions for Generation 0 then evaluate each of the solutions in the generation based on the fitness function.
Check if the termination condition is met. If the termination condition is not met, then generate the next-generation solutions.
# start with a population
best_solution=[]
population_data=generate_population(NO_OF_SOLUTION_IN_A_GENERATION,SIZE_OF_A_SOLUTION,LOWER_RANGE, UPPER_RANGE)# find the least loss in the fitness function among the population
best_individual = sort_population_by_fitness(population_data)if fitness(best_individual[0])<=1:
best_solution=best_individual[0]
else:
for gen in range(generations):
population_data=make_next_generation(population_data)
best_individual = sort_population_by_fitness(population_data)
print(best_individual)
if fitness(best_individual[0])<=1:
best_solution=best_individual[0]
print(best_solution)
breakprint("FINAL RESULT ", best_solution, " with fitness ", fitness(best_solution), "at generation ", gen)
Conclusion:
The Genetic Algorithm is a biologically inspired algorithm to solve optimization and search problems. The fittest parents’ characteristics are passed on to the next generations using selection, crossover, and mutation.
References:
Efficient Hyperparameter Optimization in Deep Learning Using a Variable Length Genetic Algorithm
AI/ML
Trending AI/ML Article Identified & Digested via Granola by Ramsey Elbasheer; a Machine-Driven RSS Bot
via WordPress https://ramseyelbasheer.io/2021/03/20/genetic-algorithm-optimization-algorithm/