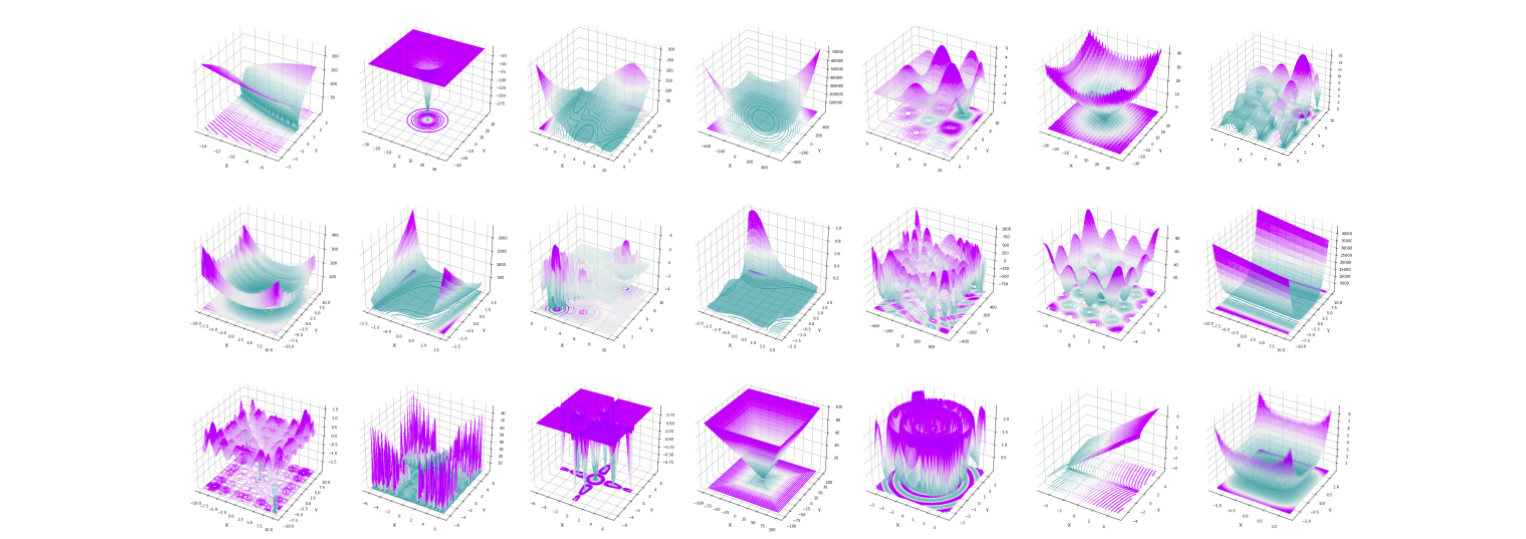
Optimization & Eye Pleasure: 78 Benchmark Test Functions for Single Objective Optimization

Original Source Here

Motivations

If you only are here for eye pleasure you can go to the Benchmark part. 😜

I was looking for a benchmark of test functions to challenge a single objective optimization. I found two great websites with MATLAB and R implementations you can find on the sources.

Yet I wanted to have this implementation in python. So I implemented these 78 functions in python in an homogeneous way to provide you an easy manner of working with them.

GitHub repository

You can find on the GitHub repository the implementation of the 78 functions as I already said. With this implementation, you can sort and filter those functions without having to know anything about these functions with a one liner.

You can also:

• plot in 3D
• plot 2D contours
• Get the latex formula
• Get the minimum global
• …

Note

• Only the 2D compatible functions are plot.
• It was a long work, so some mistakes can be found. Do not hesitate to comment or contact me if you find one of them.
• Enjoy!

Benchmark

The benchmark is alphabetically ordered except for the first function. I made a mistake in a formula and I found a beautiful function I wanted to show you. So I give my name to this function. 😄

Thevenot

continuous, non-convex, separable, differentiable, multimodal, non-random, parametric

Thevenot (image by author)

Ackley

continuous, non-convex, separable, differentiable, multimodal, non-random, parametric

Ackley (image by author)

Ackley N. 2

non-continuous, convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Ackley N. 2 (image by author)

Ackley N. 3

non-continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Ackley N. 3 (image by author)

Ackley N. 4

non-continuous, non-convex, non-separable, differentiable, multimodal non-random, non-parametric

Ackley N. 4 (image by author)

Adjiman

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Adjiman (image by author)

Alpine N. 1

non-continuous, non-convex, separable, differentiable, multimodal non-random, non-parametric

Alpine N. 1 (image by author)

Alpine N. 2

continuous, non-convex, separable, differentiable, multimodal, non-random, non-parametric

Alpine N. 2 (image by author)

Bartels

non-continuous, non-convex, non-separable, non-differentiable, multimodal, non-random, non-parametric

Bartels (image by author)

Beale

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Beale (image by author)

Bird

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Bird (image by author)

Bohachevsky N. 1

continuous, convex, separable, differentiable, non-multimodal, non-random, non-parametric

Bohachevsky N. 1 (image by author)

Bohachevsky N. 2

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Bohachevsky N. 2 (image by author)

Bohachevsky N. 3

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Bohachevsky N. 3 (image by author)

Booth

continuous, convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Booth (image by author)

Branin

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Branin (image by author)

Brent

continuous, convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Brent (image by author)

Brown

continuous, convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Brown (image by author)

Bukin N. 6

continuous, convex, non-separable, non-differentiable, multimodal, non-random, non-parametric

Bukin N. 6 (image by author)

Colville

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Colville (image by author)

Cross-in-Tray

continuous, non-convex, non-separable, non-differentiable, multimodal, non-random, non-parametric

Cross-in-Tray (image by author)

De Jong N. 5

continuous, non-convex, non-separable, differentiable, multimodal, non-random, parametric

De Jong N. 5 (image by author)

Deckkers-Aarts

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Deckkers-Aarts (image by author)

Dixon Price

continuous, convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Dixon Price (image by author)

Drop-Wave

continuous, non-convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Drop-Wave (image by author)

Easom

continuous, non-convex, separable, differentiable, multimodal, non-random, non-parametric

Easom (image by author)

Egg Crate

continuous, non-convex, separable, differentiable, multimodal, non-random, non-parametric

Egg Crate (image by author)

Egg Holder

non-continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Egg Holder (image by author)

Exponential

continuous, convex, separable, differentiable, non-multimodal, non-random, non-parametric

Exponential (image by author)

Forrester

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Forrester (image by author)

Goldstein-Price

non-continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Goldstein-Price (image by author)

Gramacy & Lee

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Gramacy & Lee (image by author)

Griewank

continuous, non-convex, separable, differentiable, non-multimodal, non-random, non-parametric

Griewank (image by author)

Happy Cat

continuous, non-convex, non-separable, differentiable, multimodal, non-random, parametric

Happy Cat (image by author)

Himmelblau

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Himmelblau (image by author)

Holder-Table

continuous, non-convex, non-separable, non-differentiable, multimodal, non-random, non-parametric

Holder-Table (image by author)

Keane

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Keane (image by author)

Langermann

continuous, non-convex, non-separable, differentiable, multimodal, non-random, parametric

Langermann (image by author)

Leon

continuous, non-convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Leon (image by author)

Levy N. 13

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Levy N. 13 (image by author)

Matyas

continuous, convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Matyas (image by author)

McCormick

continuous, convex, non-separable, differentiable, multimodal, non-random, non-parametric

McCormick (image by author)

Michalewicz

continuous, non-convex, separable, differentiable, multimodal, non-random, parametric

Michalewicz (image by author)

Periodic

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Periodic (image by author)

Perm d, beta

continuous, non-convex, non-separable, differentiable, multimodal, non-random, parametric

Perm d, beta (image by author)

Perm 0, d, beta

continuous, convex, non-separable, differentiable, non-multimodal, non-random, parametric

Perm 0, d, beta (image by author)

Powell

continuous, convex, separable, non-differentiable, non-multimodal, non-random, non-parametric

Powell (image by author)

Qing

continuous, non-convex, separable, differentiable, multimodal, non-random, non-parametric

Qing (image by author)

Quartic

continuous, non-convex, separable, differentiable, multimodal, random, non-parametric

Quartic (image by author)

Rastrigin

continuous, non-convex, separable, differentiable, multimodal, non-random, non-parametric

Rastrigin (image by author)

Ridge

continuous, non-convex, non-separable, differentiable, non-multimodal, non-random, parametric

Ridge (image by author)

Rosenbrock

continuous, non-convex, non-separable, differentiable, multimodal, non-random, parametric

Rosenbrock (image by author)

Rotated Hyper-Ellipsoid

continuous, convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Rotated Hyper-Ellipsoid (image by author)

Salomon

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Salomon (image by author)

Schaffel N. 1

continuous, non-convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Schaffel N. 1 (image by author)

Schaffel N. 2

continuous, non-convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Schaffel N. 2 (image by author)

Schaffel N. 3

continuous, non-convex, non-eparable, differentiable, non-multimodal, non-random, non-parametric

Schaffel N. 3 (image by author)

Schaffel N. 4

continuous, non-convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Schaffel N. 4 (image by author)

Schwefel

continuous, non-convex, separable, non-differentiable, multimodal, non-random, non-parametric

Schwefel (image by author)

Schwefel 2.20

continuous, convex, separable, non-differentiable, non-multimodal, non-random, non-parametric

Schwefel 2.20 (image by author)

Schwefel 2.21

continuous, convex, separable, non-differentiable, non-multimodal, non-random, non-parametric

Schwefel 2.21 (image by author)

Schwefel 2.22

continuous, convex, separable, non-differentiable, non-multimodal, non-random, non-parametric

Schwefel 2.22 (image by author)

Schwefel 2.23

continuous, convex, separable, non-differentiable, non-multimodal, non-random, non-parametric

Schwefel 2.23 (image by author)

Shekel

continuous, non-convex, non-separable, differentiable, multimodal, non-random, parametric

Shekel (image by author)

Shubert

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Shubert (image by author)

Shubert N. 3

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Shubert N. 3 (image by author)

Shubert N. 4

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Shubert N. 4 (image by author)

Sphere

continuous, convex, separable, non-differentiable, non-multimodal, non-random, non-parametric

Sphere (image by author)

Styblinski Tank

continuous, non-convex, separable, differentiable, multimodal, non-random, non-parametric

Styblinski Tank (image by author)

Sum Squares

continuous, convex, separable, differentiable, non-multimodal, non-random, non-parametric

Sum Squares (image by author)

Three-Hump

continuous, non-convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Three-Hump (image by author)

Trid

continuous, convex, non-separable, differentiable, non-multimodal, non-random, non-parametric

Trid (image by author)

Wolfe

continuous, non-convex, non-separable, differentiable, multimodal, non-random, non-parametric

Wolfe (image by author)

Xin-She Yang

non-continuous, non-convex, separable, non-differentiable, multimodal, random, non-parametric

Xin-She Yang (image by author)

Xin-She Yang N.2

non-continuous, non-convex, non-separable, non-differentiable, multimodal, non-random, non-parametric

Xin-She Yang N.2 (image by author)

Xin-She Yang N.3

continuous, convex, non-separable, differentiable, non-multimodal, non-random, parametric

Xin-She Yang N.3 (image by author)

Xin-She Yang N.4

non-continuous, non-convex, non-separable, non-differentiable, multimodal, non-random, non-parametric

Xin-She Yang N.4 (image by author)

Zakharov

continuous, convex, non-separable, non-differentiable, non-multimodal, non-random, non-parametric

Zakharov (image by author)

AI/ML

Trending AI/ML Article Identified & Digested via Granola by Ramsey Elbasheer; a Machine-Driven RSS Bot

via WordPress https://ramseyelbasheer.wordpress.com/2020/12/31/optimization-eye-pleasure-78-benchmark-test-functions-for-single-objective-optimization/