How to improve your linear regression with basis functions and regularization



Original Source Here

How to improve your linear regression with basis functions and regularization

Introduction to basis functions and regularization with theory and Python implementation

Illustration of increasing regularization on a model that overfits. Image by author.

Contents

This post is a part of a series of posts that I will be making. You can read a more detailed version of this post on my personal blog by clicking here. Underneath you can see an overview of the series.

1. Introduction to machine learning

2. Regression

Basis functions

In the previous post we discussed the linear regression model

We say that a model is linear if it’s linear in the parameters not in the input variables. However, (1) is linear in both the parameters and the input variables, which limits it from adapting to nonlinear relationships. We can augment the model by replacing the input variables with nonlinear basis functions of the input variables

where

By using nonlinear basis functions it is possible for h to adapt to nonlinear relationships of x, which we will see shortly — we call these models linear basis function models.

We already looked at one example of basis functions in the first post of the series, where we augmented the simple linear regression model with basis functions of powers of x, i.e.,

Another common basis function is the Gaussian

Following the same derivation as in the previous post, we find the maximum likelihood solutions for w and α to be

where

The image below shows a linear basis function model with M-1 Gaussian basis functions. We can see that increasing the number of basis functions makes a better model, until we start overfitting.

Illustration of the effect of using M−1 Gaussian basis functions (plus the intercept). Image by author.

Implementation

Using the same dataset as in the previous posts, we get the implementation below.

Regularization

We briefly ran into the concept of regularization in the post on Bayesian inference, which we described as a technique of preventing overfitting. If we look back at the objective function we defined in the previous post (augmented with basis functions) we can introduce a regularization term

where q>0 denotes the type of regularization, and λ controls the extent of regularization.

The most common values of q are 1 and 2, which are called L1 regularization and L2​ regularization respectively. We call it lasso regression when we use L1​ regularization, and ridge regression when we use L2​ regularization.

The objective function of ridge regression

is especially convenient as it is a quadratic function of w and therefore has a unique global minimum. The solution to which is

where α stays the same as without regularization, since the regularization term has no influence on it.

When we introduce regularization, the process of model selection goes from finding the appropriate number of basis functions to finding the appropriate value for the regularization parameter λ.

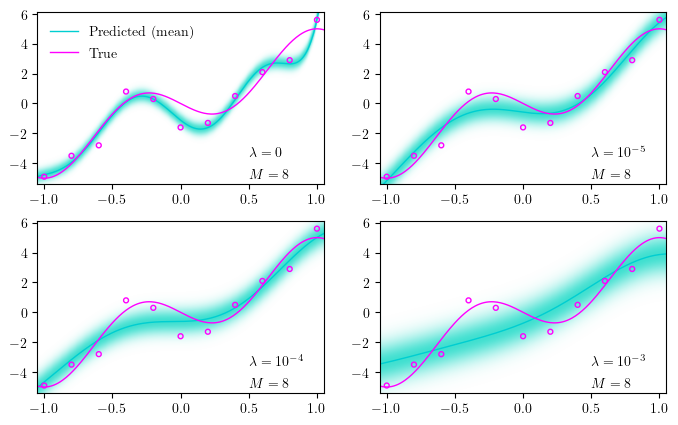
The image below shows a linear basis function model with varying values for λ, while keeping the number of basis functions constant M=8. We can see that even though we overfit to begin with, we can adjust the regularization parameter λ to prevent it — in fact, we start underfitting when the regularization is too much. Another interesting thing to see is that our uncertainty increases along with the regularization.

Illustration of increasing regularization for a model that is overfitting. Image by author.

Implementation

Summary

  • What makes a model linear is that it’s linear in the parameters not the inputs.
  • We can augment linear regression with basis functions yielding linear basis function models.
  • Polynomial regression is a linear basis function model.
  • Regularization is a technique of preventing overfitting.
  • There are different kinds of regularization in linear regression such as L1​ and L2 regularization.

AI/ML

Trending AI/ML Article Identified & Digested via Granola by Ramsey Elbasheer; a Machine-Driven RSS Bot



via WordPress https://ramseyelbasheer.io/2021/03/25/how-to-improve-your-linear-regression-with-basis-functions-and-regularization/

Popular posts from this blog

I’m Sorry! Evernote Has A New ‘Home’ Now

Image
Original Source Here My Apologies! I was critical about the grandfather of all apps — Evernote a few months back when I wrote Why is Evernote losing its Ground? on Medium. With that said, I also wrote another story on Evernote in November of last year — Has Evernote Made A Comeback After Years Of Stagnation? This was the time when Ian Small and his team were making inroads into the technology and strategically making enhancements and revamping the app across all platforms. Evernote Is At A War-front And Wants To Prove A Point. I must h ave written this in my earlier blogs but just to re-iterate — I have been and am an avid user of Evernote since 2009 and is a part of my life for planning my daily life, projects, content writing, and almost everything. Recently, Evernote has launched its HOME or you may call it a DASHBOARD that provides its users a one-stop place to get access to their important and critical notes and also provides a few AI-enabled capabilities that I wil...
Read more

Jensen Huang: Racism is one flywheel we must stop

Image
https://venturebeat.com/wp-content/uploads/2021/07/jensen-huang.jpg?w=1200&strip=all Original Source Here All the sessions from Transform 2021 are available on-demand now. Watch now. Jensen Huang , CEO of Nvidia , received the distinguished lifetime achievement award by the Asian American Engineer of the Year from the Chinese Institute of Engineers (CIE) group. And in his acceptance speech, he made a rare comment beyond Nvidia’s business matters: “Racism is one flywheel we must stop.” The comments came at the end of an acceptance speech where he thanked the group for its award, an annual gathering that recognizes outstanding Asian American scientists, engineers and role models. In a virtual ceremony, Huang was awarded for his contributions as “a visionary and innovator in parallel computing technology that accelerates the realization of AI computing.” He also spoke of his experience as an immigrant and an Asian American. “It is strange to accept a lifetime achievem...
Read more

Fully Explained DBScan Clustering Algorithm with Python

Image
Original Source Here Fully Explained DBScan Clustering Algorithm with Python Unsupervised learning in machine learning on density-based clusters Clustering In unsupervised Learning. A photo by Author In this article, we will discuss the machine learning clustering-based algorithm that is the DBScan cluster. The approach in this cluster algorithm is density-based than another distance-based approach. The other cluster which is distance-based looks for closeness in data points but also misclassifies if the point belongs to another class. So, density-based clustering is suited in this kind of scenario. The cluster algorithms come in unsupervised learning in which we don’t rely on target variables to make clusters. In a cluster, the main concern is on maximum dense connected points. The density-based clustering can be useful in arbitrary shapes even with noise. The working function of the density-based cluster is shown below: We select a random data point. Then it will ...
Read more