可解釋 AI (XAI) 系列 — SHAP



Original Source Here

SHAP 如何解釋模型？

SHAP (SHapley Additive exPlanations) 是一種機器學習的可解釋方法，再介紹 SHAP 之前需要先介紹什麼是 Shapley Values

Shapley Values

Shapley Values 是博弈論大師 Lloyd Stowell Shapley 基於合作賽局理論 (cooperative game theory) 提出來解決方案，這種方法根據玩家們在遊戲中所得到的總支出，公平的分配總支出給玩家們

  • 玩家們 → features value of the instance
  • 遊戲 → model
  • 總支出 → prediction

Shapley Values 透過 S 中玩家的值函數 val 定義的：

  • x_1, …, x_p 為建立模型所使用的所有特徵，p 為所有的特徵數量。
  • S 為排除 x_j (想看這個玩家的貢獻程度) 的子集合。
  • val(S) 是對於集合 S 的預測值減去期望值 (平均預測值)。

這些公式是怎麼來的？我們來實際看一個例子就可以明白了。

A concrete example

假設工程師們需要合作寫一個 project，共計 100 行 code，圖一 顯示了工程師期望產出 code 的行數，也就是對應的 val(S)

圖一，工程師期望產出 code 的行數

而我們想要計算出 x1 這位工程師的 Shapley values，也就是他的貢獻值該如何計算呢？我們來看一下 圖二 的計算流程，三位工程師，因此會有六種排列組合，需要針對每種情形來計算出 x1 的 Shapley value，因為先後順序是會影響他的貢獻值的，接著再把六個值加總平均就可以得到 x1 的 Shapley values 了。

圖二，x1 的 Shapley values 計算流程

那我們就可以知道為什麼 Shapley values 的公式要這樣計算了，我們在這邊帶入公式給各位看，可以看到得到得結果都是 34.17

最後我們可以分別計算出 x2 和 x3 的 Shapley values，如 圖三 所示，最後得到 x1 是 34.17, x2 是 41.7, x3 是 24.17，可以發現這三個值相加其實就等於 100 行 code，簡單來說，這個 Shapley values 其實就是想要衡量個別的特徵對模型的貢獻程度為何，而不受到其他特徵的影響。

圖三，x1, x2, x3 的 Shapley values 計算過程

讀者看到這邊可以發現，其實這樣計算 Shapley values 是很花計算資源的，而且當 feature values 比較多時，可能的聯盟數量呈指數性增加，因此對於計算精確的 Shapley value 是一大問題，對於這個問題 Štrumbelj et al. 提出蒙地卡羅採樣的近似值 (Shapley Sampling)

  • x_(+j)=(x_1, …, x_(j-1), x_j, z_(j+1)…z_p)，意思是除了特徵值 x_j 以外，其他不在聯盟內的特徵值被來自隨機數據點 z 的特徵值替換。
  • x_(-j)=(x_1, …, x_(j-1), z_j, z_(j+1)…z_p)，表示連特徵值 x_j 都要替換。

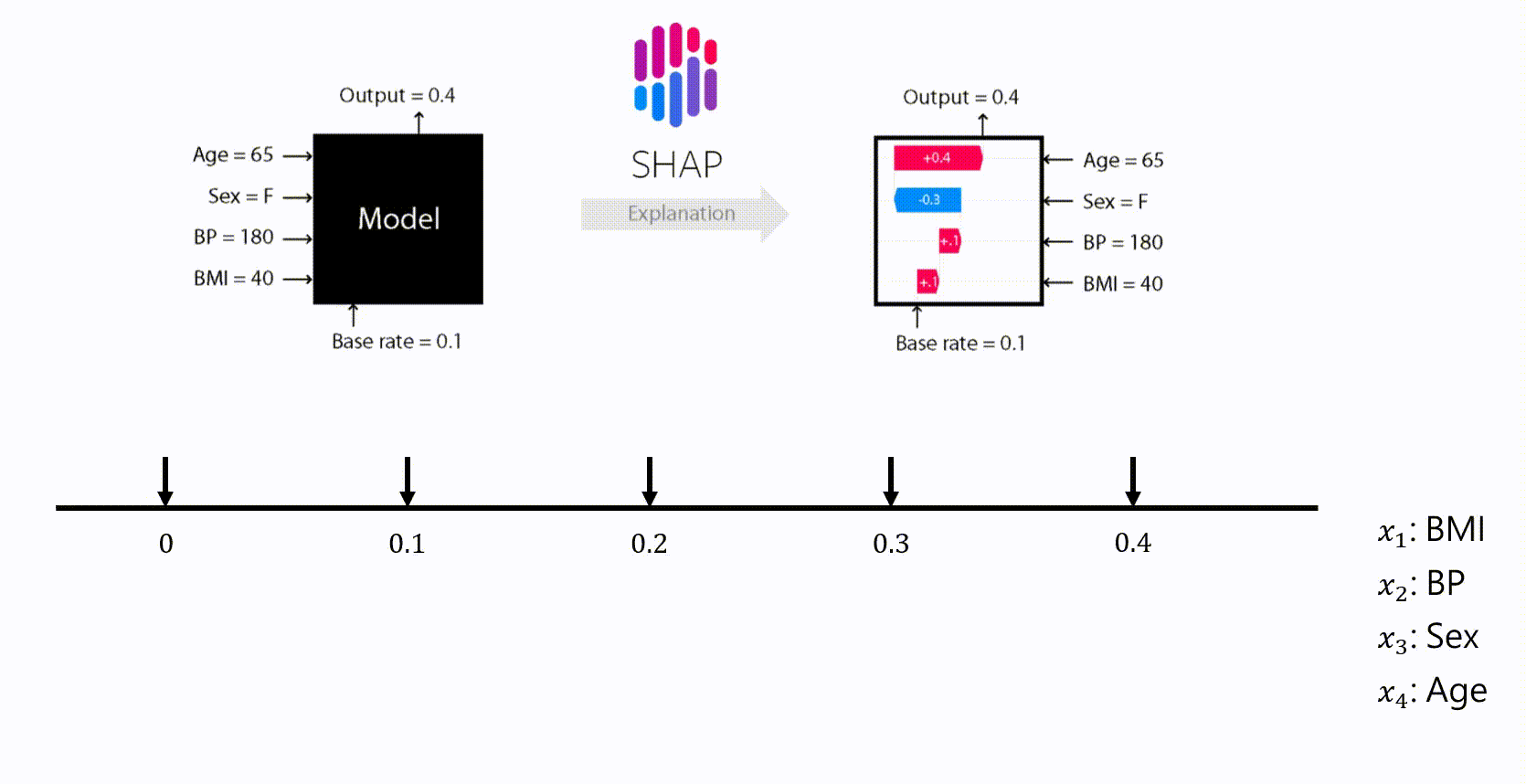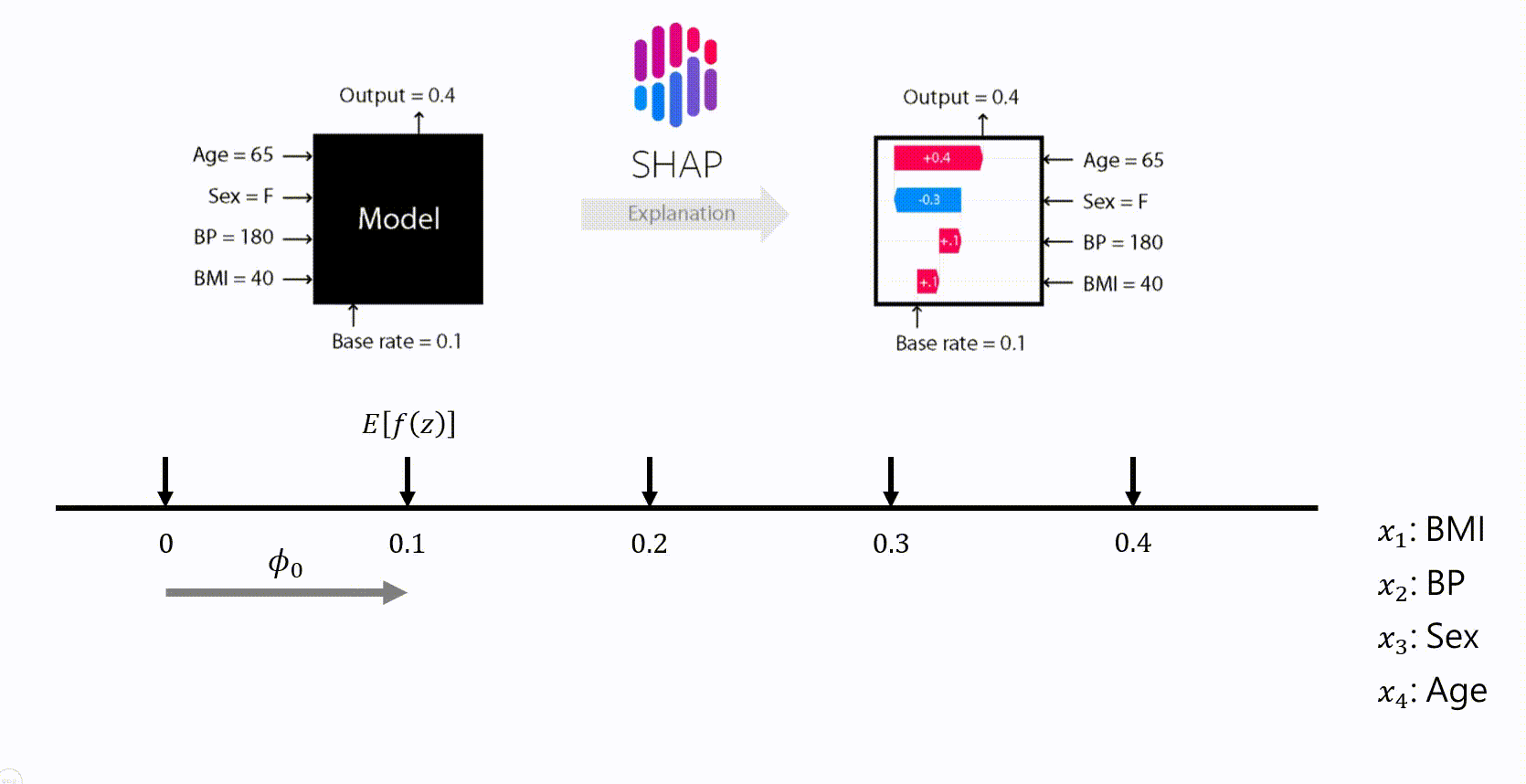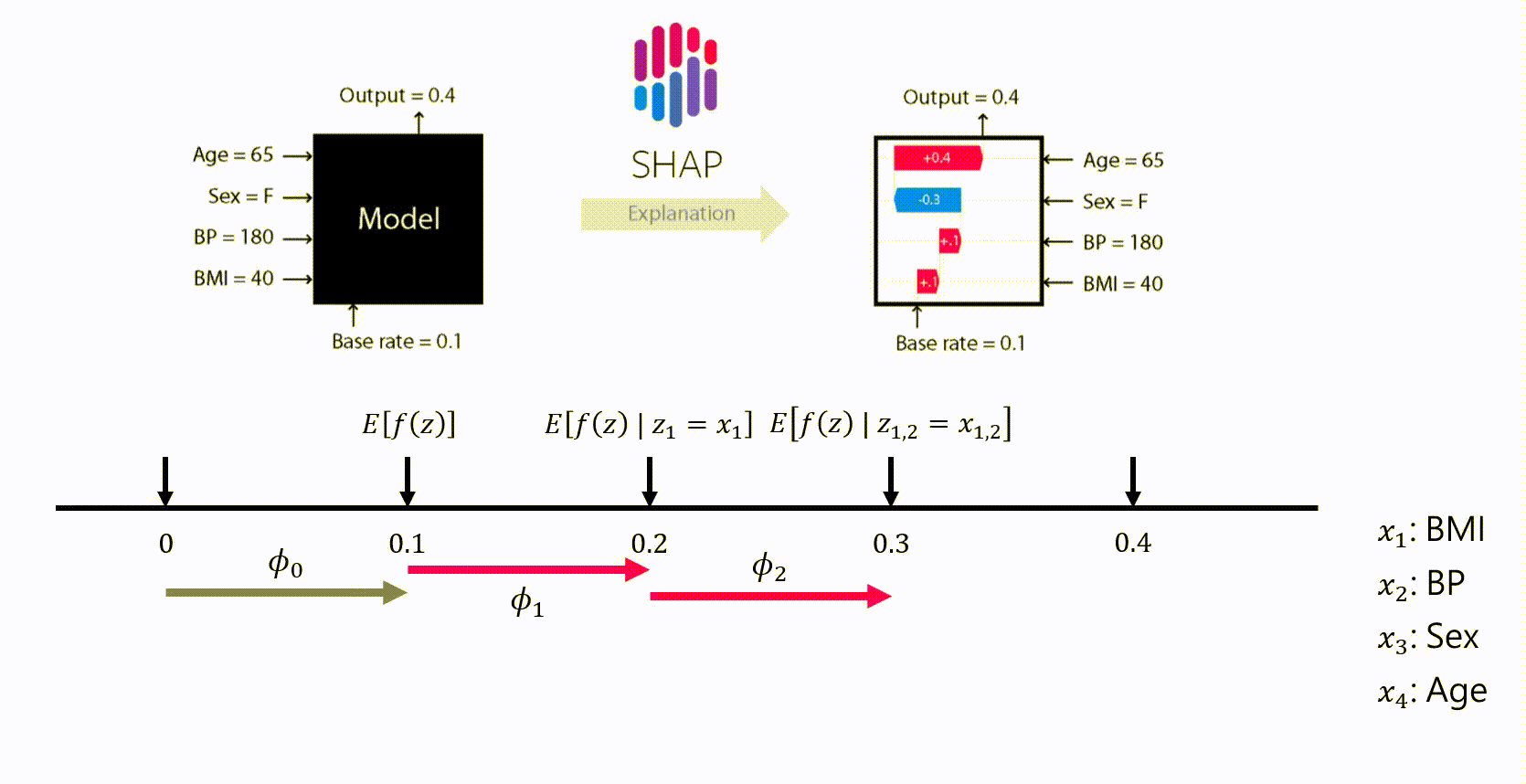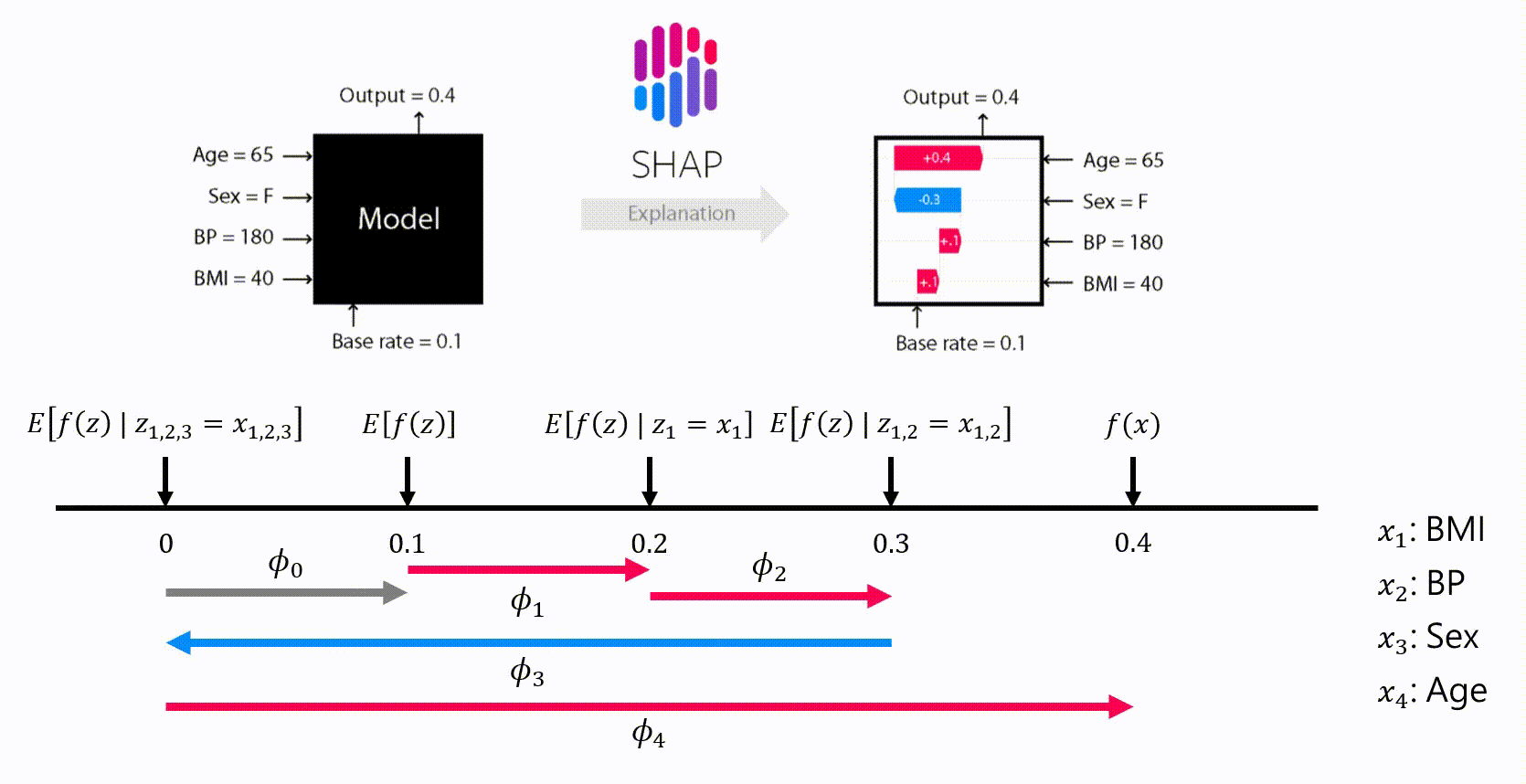
除了這個方法，還可以使用 SHAP (SHapley Additive exPlanations)來估計 Shapley values，SHAP 將模型的預測值解釋為每個輸入特徵的歸因值之和。換句話說，就是計算每一個特徵的 shapley value，依此來衡量特徵對最終預測值的影響。用公式表示：

  • g(z^′ ) 為被簡化的可解釋的模型
  • z^′ 表示相應特徵是否存在 (1 或 0)，M 是輸入特徵的個數，因此可以表示成 z^′∈{0, 1}^M
  • ϕ_i 代表我們要求的 Shapley value
  • ϕ_0 代表平均值

Kernel SHAP

圖四，Kernel SHAP 的計算流程

圖四 說明了他的計算流程，下面為各位詳細說明：

Step 1:

我們只想要求 Age 的 Sapley values，而 Weight 和 Color 都先不要求，因此將 Age, Weight, Color 的 z 設為 (1, 0, 0)

Step 1

Step 2:

我們取得 DATA 裡的值，假設有一筆資料的 Age, Weight, Color 為 0.5, 20, Blue，由於我們 Age, Weight, Color 的 z 設為 (1, 0, 0)，因此只須保留 Age 的正確性 (0.5)，其他兩個都隨機替代其他資料存在的值，例如 Weight 從 20 換成 17、Color 從 Blue 換成 Pink，注意，17 和 Pink 必須要是 DATA 裡有存在的值哦，不能隨機填。

Step 3:

Kernel SHAP 中權重的計算根據 Simplified Features 中 0 或 1 的數量，若有很多 0 或是很多 1，我們取較高的權重，若 0 和 1 的數量相近則取較低的權重。

Step 4:

最後再根據資料來 fit 一個 weighted linear model，而獲得的 weight 其實就是特徵對應的 Shapley values

總結

SHAP 是一個很有公信力的可解釋性工具，因為背後有強大的數學理論支持它，而 shap 在程式上的使用和畫面的呈現也很簡單直覺，有興趣的可以參考下面兩篇實做文章

Explain Your Machine Learning Model by SHAP. (Part 1)

Explain Your Machine Learning Model by SHAP. (Part 2)

AI/ML

Trending AI/ML Article Identified & Digested via Granola by Ramsey Elbasheer; a Machine-Driven RSS Bot



via WordPress https://ramseyelbasheer.io/2021/07/08/%e5%8f%af%e8%a7%a3%e9%87%8b-ai-xai-%e7%b3%bb%e5%88%97%e2%80%8a-%e2%80%8ashap/

Popular posts from this blog

I’m Sorry! Evernote Has A New ‘Home’ Now

Image
Original Source Here My Apologies! I was critical about the grandfather of all apps — Evernote a few months back when I wrote Why is Evernote losing its Ground? on Medium. With that said, I also wrote another story on Evernote in November of last year — Has Evernote Made A Comeback After Years Of Stagnation? This was the time when Ian Small and his team were making inroads into the technology and strategically making enhancements and revamping the app across all platforms. Evernote Is At A War-front And Wants To Prove A Point. I must h ave written this in my earlier blogs but just to re-iterate — I have been and am an avid user of Evernote since 2009 and is a part of my life for planning my daily life, projects, content writing, and almost everything. Recently, Evernote has launched its HOME or you may call it a DASHBOARD that provides its users a one-stop place to get access to their important and critical notes and also provides a few AI-enabled capabilities that I wil...
Read more

Jensen Huang: Racism is one flywheel we must stop

Image
https://venturebeat.com/wp-content/uploads/2021/07/jensen-huang.jpg?w=1200&strip=all Original Source Here All the sessions from Transform 2021 are available on-demand now. Watch now. Jensen Huang , CEO of Nvidia , received the distinguished lifetime achievement award by the Asian American Engineer of the Year from the Chinese Institute of Engineers (CIE) group. And in his acceptance speech, he made a rare comment beyond Nvidia’s business matters: “Racism is one flywheel we must stop.” The comments came at the end of an acceptance speech where he thanked the group for its award, an annual gathering that recognizes outstanding Asian American scientists, engineers and role models. In a virtual ceremony, Huang was awarded for his contributions as “a visionary and innovator in parallel computing technology that accelerates the realization of AI computing.” He also spoke of his experience as an immigrant and an Asian American. “It is strange to accept a lifetime achievem...
Read more

Fully Explained DBScan Clustering Algorithm with Python

Image
Original Source Here Fully Explained DBScan Clustering Algorithm with Python Unsupervised learning in machine learning on density-based clusters Clustering In unsupervised Learning. A photo by Author In this article, we will discuss the machine learning clustering-based algorithm that is the DBScan cluster. The approach in this cluster algorithm is density-based than another distance-based approach. The other cluster which is distance-based looks for closeness in data points but also misclassifies if the point belongs to another class. So, density-based clustering is suited in this kind of scenario. The cluster algorithms come in unsupervised learning in which we don’t rely on target variables to make clusters. In a cluster, the main concern is on maximum dense connected points. The density-based clustering can be useful in arbitrary shapes even with noise. The working function of the density-based cluster is shown below: We select a random data point. Then it will ...
Read more