Support Vector Machine (SVM) Introduction — Machine Learning
Original Source Here
In this particular example that we have considered, we are expecting the output of the classifier equation to be either a positive number indicating the data point belongs to a positive class or a negative number indicating the data point belongs to a negative class. If any point exactly on the decision boundary, then the output of the classifier would be zero, and hence, the equation of the decision boundary is:
Similarly, classifier equations for marginal hyperplanes:
Let’s not blindly believe in it. We shall go ahead and derive why the output of the equation is either positive or negative.
Consider the above problem where the decision boundary passes through the origin and hence intercept is zero and its slope is +1. A single data point on each side of the hyperplane represents both the positive and negative classes. Substituting the values in the equation of the hyperplane:
Any point below the hyperplane will always be positive, and above the hyperplane will be negative.
Next, the margin has to be maximized to find the optimal decision boundary. Consider the negative support vector as point x1 and the positive support vector as point x2. The margin would be simply the difference between x1 and x2. Let’s arrive at this equation with the help of solving the linear equations. Mathematically, we have two equations with two unknowns (x1 and x2). To find the unknowns, subtract one equation from another.
To find x1–x2, w has to be sent to the equation’s left-hand side, which gives 2 over w. It is already known that w is a vector, and vectors can not be divided directly like a scalar value. The equivalent would be to divide both sides by the length of w, that is, the magnitude of that norm of w.
When w is divided by its normal form, it still points in the same direction, but the magnitude would be 1 unit equivalent to scalar 1. Hence
Now that we have arrived at the equation for the margin, it is considered the optimization function that needs to be maximized using optimization algorithms like gradient descent. Optimization algorithms work best when finding the local minimum, hence to ease the problem, minimizing the reciprocal of x1–x2 can be used as an optimization function, which is the norm of w over 2.
It is also possible that the SVM model can have some percentage of error, meaning, misclassification of new data, and that has to be integrated into our optimization function, where Ci indicates the number of error points, in other words, the number of misclassified data points and summation of the distance between the marginal hyperplane and the misclassified data point.
Terminology Alert
1. Hard Margin: The margin which is intolerant to any errors is known as hard margin. It is sensitive to outliers, and a single outlier can affect the decision boundary.
2. Soft Margin: The margin which can consider some percentage of error is known as soft margin. Insensitive to outliers.
Summary:
It is not mandatory to understand the math entirely. It is ok if you could not follow the derivation. Fundamentally, it essential to know that SVM creates a hyperplane that acts as a decision boundary to classify the data points, and to find the right boundary, two hyperplanes are considered where the distance between them has to be maximum.
SVM Kernels
SVM is easy when building a hyperplane for linearly separable data points. However, it is much more challenging when the data is non-linearly separable. As discussed, SVM kernels help in converting low dimensional non-linearly separable data points into high dimensional linearly separable data points. There are three popularly known SVM kernels:
- Polynomial
- Radial Basis Function (RBF)
- Sigmoid
Let’s build upon the intuition of how kernels work by converting 1-d non-linearly separable data into 2-d linearly separable data.
Consider the above data points, and it is an example of the binary classification ( 1 and 0). It is impossible to draw a linear line that can separate the two classes. Applying a transformation on each point will convert 1-d data points into 2-d, helping build a decision boundary. Here, the transformation function would be:
That is, square each of the data points and plot the result as the second dimension (y-axis).
Original data points are plotted on the x-axis, and transformed data points(x-square) are plotted on the y-axis. Now, the data points are easily separable by drawing a linear hyperplane. Visualizing higher dimensional data points would be challenging. However, SVM kernels work similarly with higher dimensional data points, too, convert low dimensional data into high dimensional data so that they transform into linearly separable datapoints.
Implementation
Implementation in python is pretty straightforward. Python being open source provides us ready-made packages to implement several machine learning algorithms, and SVM is no exception. Using the SVC package from sklearn provides several advantages and flexibility. SVC stands for Support Vector Classification, and the implementation is based on libsvm and a wrapper around SVM. Let’s import the necessary packages.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns#classic datasets from sklearn library
from sklearn import datasetsfrom sklearn.model_selection import train_test_split#Support Vector Classification-wrapper around SVM
from sklearn.svm import SVC#different matrices to score model performance
from sklearn import metrics
from sklearn.metrics import classification_report,confusion_matrix
For implementation purposes, we will be using a wine dataset. It is a multiclass dataset with 3 classes, 178 total samples, and 13 features. This data results from a chemical analysis of wines grown in the same region in Italy but derived from three different cultivars. The analysis determined the quantities of 13 constituents found in each of the three types of wines [4].
Let’s load the wine data from the sklearn library. Since the data is being loaded from sklearn, it would be easier to work with it if we store it into a DataFrame.
#loading WINE dataset
cancer_data = datasets.load_wine()#storing into DataFrame
df = pd.DataFrame(cancer_data.data, columns = cancer_data.feature_names)
df['target'] = cancer_data.target
df.head()
Performing analysis by plotting graphs will help in understanding the dataset better. It is always advised to check if data is balanced, that is, if all the target classes have the same number of records.
#analysing target variable
sns.countplot(df.target)
plt.show()
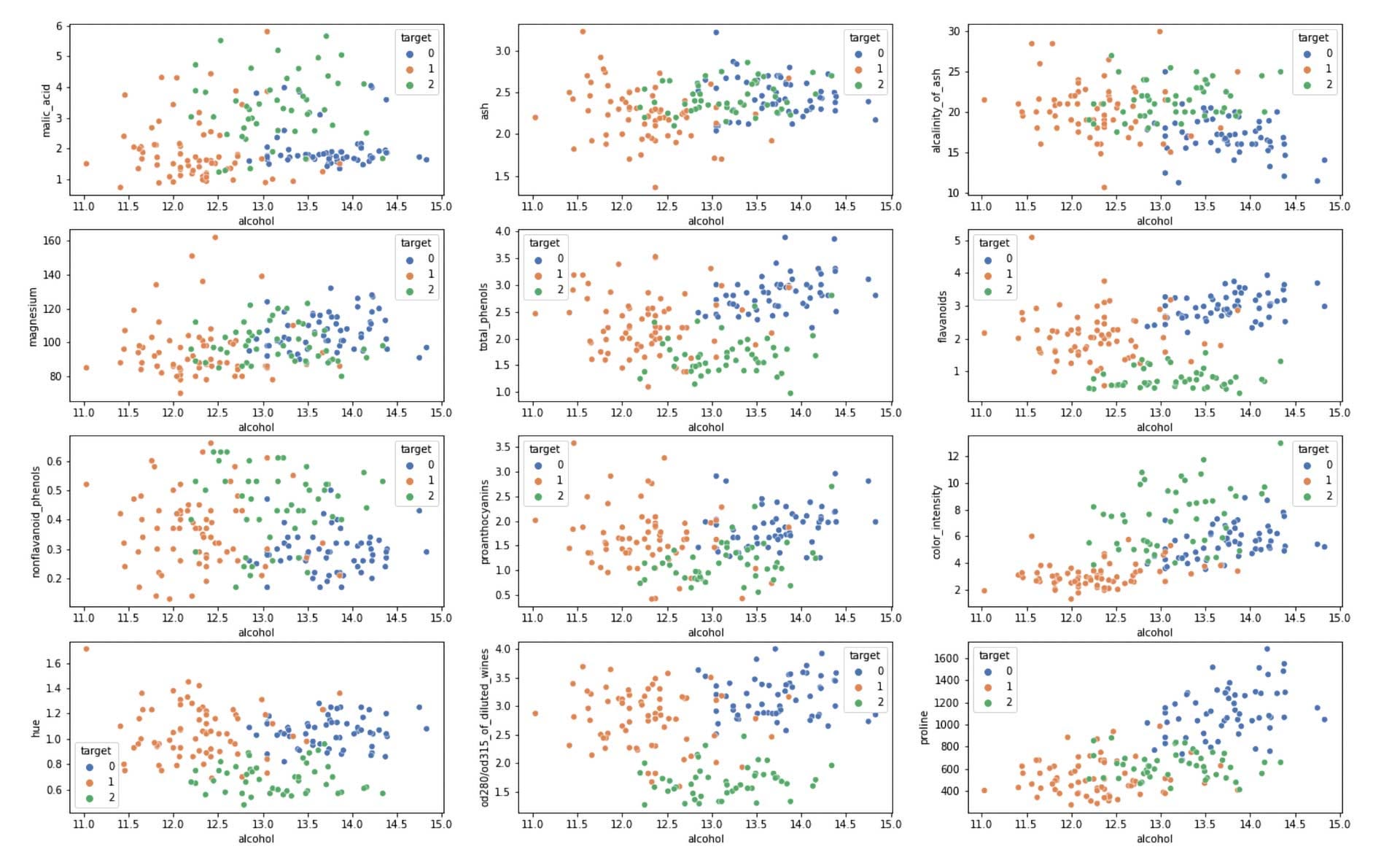
Along with being a multiclass classification problem, it also represents an imbalanced classification problem. Next, let’s check if our data is linearly separable or not. This will give an initial inference to decide what type of kernel will best classify the data. For simplicity, let’s plot every feature against alcohol and color the data points concerning their class.
#visualizing datapoints separability
fig, axes = plt.subplots(6, 2, figsize=(22,14))
axes = [ax for axes_rows in axes for ax in axes_rows]
columns = list(df.columns)
columns.remove('target')
columns.remove('alcohol')#looping through every columns of data
#and plotting against alcohol
for i, col in enumerate(columns):
sns.scatterplot(data=df, x='alcohol', y=col, hue='target', palette="deep", ax=axes[i])
AI/ML
Trending AI/ML Article Identified & Digested via Granola by Ramsey Elbasheer; a Machine-Driven RSS Bot
via WordPress https://ramseyelbasheer.io/2021/04/08/support-vector-machine-svm-introduction%e2%80%8a-%e2%80%8amachine-learning/