Predicting the Remaining Useful Life of Turbofan Engine
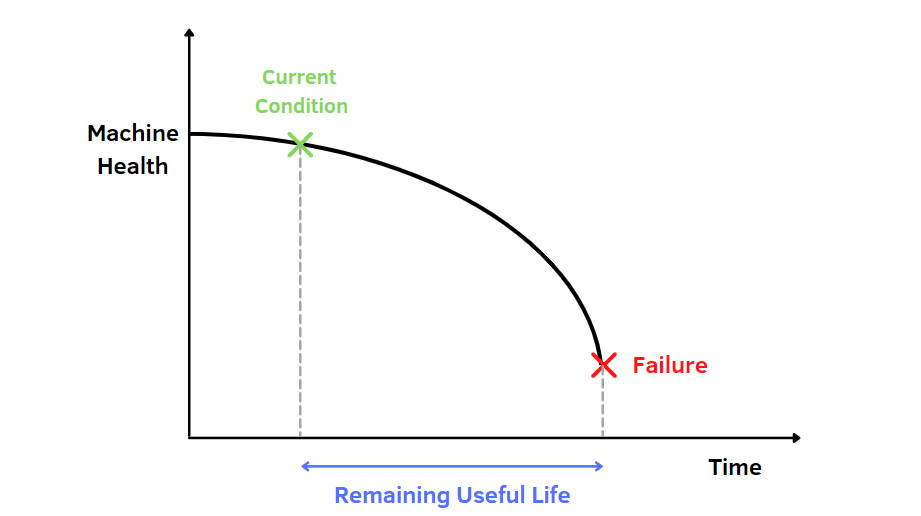
Original Source Here
1. Import Data
Let’s import the libraries that will be needed in the following steps:
Once the libraries are imported, we can load the dataset PHM08. The dataset is available in Kaggle, already divided into training and test sets, and is composed of 26 columns:
- Unit Number
- Time in Cycles
- Operational Settings 1,2,3
- Sensor Measurements 1,…,21
Each row represents a snapshot taken during a single operational cycle.
After we created the vector with all the names of the columns, we can import the training set, provided as a text file with columns separated by spaces.
From the output, we can observe that there are many rows with the same unit number, called unit_id. For example, the rows with unit_id=1 represent the life cycle of that particular engine until the degradation state, observed within the time, that is referred to by the variable time_cycle. In general, the last cycle in each engine represents the failure point.
When time_cycle is equal to 1, the engine is always healthy, while in the other time cycles the performance of the engine will get worse. Then, the engine with unit_id=1 fails at time cycle 192. There are 100 engines in total in all the training set. Moreover, it’s already possible to observe that some sensor measurements increase over time and will contribute to building the predictive algorithm, while other measurements remain constant or change very slightly.
Now, we do the same thing for the test set and the RUL values of the test set. The test data has a similar structure to the training data. The only difference is that we don’t know when the failure occurs. The RUL_FD001.txt provides the RUL values only for the last time cycle of each engine. In the case of the engine with unit_id equal 1, it can run other 112 time cycles before it fails.
Both training and test sets contain the feature variables, but the target variable is missing. We need it for our supervised task, to understand how far the predictions are from the real values.
2. Compute Remaining Useful Life
There are many methods to calculate the Remaining Useful Life. One way is to first obtain the maximum time cycle for each unit id and then do the following difference:
To find the Maximum time cycle for each unit id of the training data, we need to group the data by unit id and filter by time cycle. Then, we create a dataframe composed of two columns, where a maximum time cycle corresponds to a unique unit id.
After we merge the last data frame obtained and the training set. In this way, we can include the RUL as target variable.
From the output, we can see the data with unit id equal to 1 have the RUL that decrease over time. The smaller the RUL is, the higher the risk of failure is. When the RUL is zero, it means that the engine failed.
Once we calculated the RUL for the training data, we need to add the RUL column for the test data too. The sizes of test data and RUL of the corresponding test set are different since the RUL_FD001.txt provides the RUL values only for the last time cycle of each engine. So, the idea is to assign the RUL value to the last row of each unit id and in each row above we add one until we reach the first time cycle of that particular engine.
To check if the calculation is correct, it’s good to compare the RUL true values and the test data with unit id equal to a certain number:
In this example, the RUL is equal to 91 for the last time cycle of the engine with unit id=5 looking at the y_true dataframe. In the updated test data, we have the same value in the last row of that specific engine, while in the rows above we incremented the RUL each time of one unit.
3. Feature Selection
As I said before, different sensors have different behaviour over time. So, we need sensors more sensitive to the degradation process to improve the performance of the prediction model. To find the most significant variables, we can look at the correlation matrix:
From the correlation matrix, we can observe that there are some variables that have always the NAN coefficient with the other variables: the operational setting 3, sensor measurement 1, 5,10, 16, 18 and 19. These NAN values can be interpreted as the absence of correlation between the variables. For example, the NAN correlation coefficient between the time cycle and sensor measurement 1 means that when the time_cycle change, the sm_1 doesn’t change. This implies that we should remove these variables from the training and test sets. To highlight these aspects, we can also plot the RUL in relationship with the feature variables.
Above, I show only some of the plots obtained. If you take a look at these graphical tools, it’s clear that some of the sensor measurements don’t show significant change when the Remaining Useful Life change. Then, these sensor measurements won’t be selected in the model.
4. Max-Min Normalization
Once we selected only the significant features of the dataset, we can normalize the data. This step is important to avoid dependence on the choice of the measurements units. Indeed, the feature variables have different ranges of values and may reduce the performance of the model. A way is to transform the data to fall within a smaller range between -1 and 1. The technique applied is the max-min normalization, available in sklearn module.
After the max-min normalization, we can split the training and test sets into feature and target variables.
5. Predictive Model
After many steps, we can finally build a model on the training data. The chosen model is Gradient Boosting, which is an ensemble of decision trees. It’s interesting to apply it because it’s characterized by powerful performances and high interpretability. Let’s import the libraries:
Now we can train the model on the training set and evaluate it on the test set:
The performance of the model seems quite good, even if there is difference between the performances on training and test sets. Another tool to interpret the performance of the model is the “feature importances”, which are scores that represent how each feature variable contribute to the model. So, we can plot the feature importance:
The feature that most contribute to the model is time_cycle. Other important variables are sensor measurement 11, 4, 9, while the remaining features are less relevant in the model. It seems clear that Operational setting 1 and 2 are not significantly involved in the model and it would be better to try to remove them from both training and test sets.
Another way to have a more impartial performance of the model would be to perform k fold cross validation. The idea to divide the dataset into k parts, k-1 to train and the remaining one to test, allowing to avoid overfitting. Indeed, there are surely portions of the dataset not representative and may lead to misunderstanding results.
The average root mean squared error seems quite better than the one obtained before (60.4). Then, we achieved a better performance by diving the dataset into training and test more times.
AI/ML
Trending AI/ML Article Identified & Digested via Granola by Ramsey Elbasheer; a Machine-Driven RSS Bot
via WordPress https://ramseyelbasheer.io/2021/03/21/predicting-the-remaining-useful-life-of-turbofan-engine/