Implementing the shortest Path Djikstra’s algorithm on real data and comparing the result on…
Original Source Here
Implementing the shortest Path Djikstra’s algorithm on real data and comparing the result on Google Maps
Dijkstra’s algorithm or Dijkstra’s Shortest Path First algorithm is used to find the shortest path between two points, which may represent road networks. The points or nodes are usually represented in a graph (Thanks to Wikipédia for the graph GIF below).
The most common variant of this algorithm fixes a single node as the “source” node and finds the shortest paths from the source to all other nodes. For this reason, it is classified as search, greedy algorithm with dynamic programming and can be used to understand the fundamentals of distance-time matrix of #googlemaps, #uber and other similar apps.
The full description of this algorithm can be found here. Below the iterative process of finding the shortest path between the source node and other nodes
Here I will implement this algorithm on real data and compares the result to the one suggested by #GoogleMaps. Below the map of Rio de Janeiro downtown is shown, with the starting point as Candelária VLT station and end point as Orla Prefeito Luiz Conde. As per GoogleMaps, the suggested walking time is 8 min.
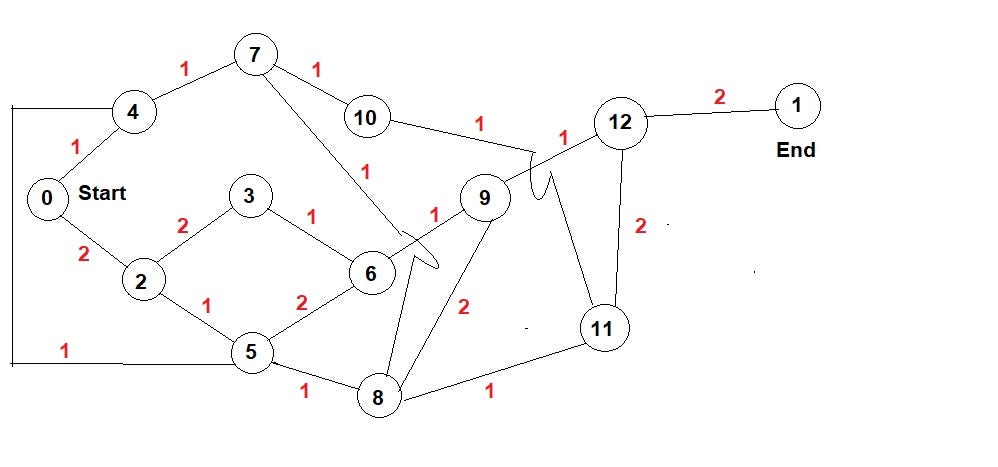
In order to implement this algorithm, I will add several nodes or intersections between the starting and ending points. Some of them may reduce or increase the walking time.
Before proceeding to the code, I would like to thank Aashish Barnwal and GeekforGeeks for providing enough explaination on the codes. Below the graph of Rio de Janeiro downtown that will be used to implement the algorith is depicted. As previously mentioned, I added 11 nodes between the starting and ending points with their respective walking times (in minutes).
The graph above can be also represented in a matrix form known as distance-time matrix, where the rows and columns are the nodes, and the values in the matrix represent the distance or time values between two nodes.
Using GoogleMaps, I found that the min and max walking time to reach the end point are 8 and 9 minutes respectively. With a quick glimpse in the graph, I can extract one of the shortest paths (0 -> 4 -> 7 -> 8-> 11 -> 12 -> 1) and one of the longest paths (0 -> 2-> 3-> 6-> 9-> 12 -> 1).
Let’s suppose that the min and max walking time are unknown, and the objective is to find the min walking time using Djikstra’s algorithm. The result below shows the shortest paths walking time to reach each nodes. Note that the end point is node 1.
As per the result, I can conclude that, although GoogleMaps might use advanced artificial intelligence tools to find the shortest paths, Djikstra’s algorithm might be used to understand the fundamentals of this class of algorithms.
The full code of this algorithm can be found here.
AI/ML
Trending AI/ML Article Identified & Digested via Granola by Ramsey Elbasheer; a Machine-Driven RSS Bot
via WordPress https://ramseyelbasheer.wordpress.com/2021/03/08/implementing-the-shortest-path-djikstras-algorithm-on-real-data-and-comparing-the-result-on/